02 - binary system

Logic

Logic is a subfield of mathematics. In computer science, boolean algebra plays a huge role - it is used as the theoretical basis of constructing devices that work in the binary system.

When humans add numbers (using decimal system) they do so by applying a set of rules over consecutive digits[1]. Computers do the same task but in the binary system. The rules are applied on the basis of boolean algebra.

In boolean algebra, there are only 2 possible states: false and true. 0 and 1. No and yes. Negative and positive. ...and whatever else you like to call them.

Boolean algebra by itself is not enough to perform computations, but it's a building block for more complex systems.

In this algebra, there are 3 basic operations: NOT, OR and AND. We can think of them as functions - mechanisms which take certain input to provide certain output.

NOT is the simplest of them. It simply reverses the value:

The other 2 are 2-argument functions:

• OR is true when x or y is true

• AND is true when x and y is true

• OR is sometimes referred to as boolean addition or maximum function

• AND is sometimes referred to as boolean multiplication or minimum function

Out of these functions, it's possible to construct more complex ones:

• x NOR y is equivalent to NOT (x OR y)

• x NAND y is equivalent to NOT (x AND y)

• x XOR y (exclusive OR) is equivalent to:

  • (x OR y) AND NOT (x AND y)

  • (x OR y) AND (NOT x OR NOT y)

• x NXOR y is equivalent to NOT (x XOR y) which is also equivalent to:

  • (x AND y) OR NOT (x OR y)

  • (x AND y) OR (NOT x AND NOT y)

All of these functions are often referred to as logic gates.

Numberphile has made a video explaining how you can build logic gates using dominos. Through junctions and collisions you can imitate elements such as diode and transistor. Later they showcase a 10000 domino circuit that adds 2 4-bit integers.

Below is an example of the 7400 chip which contains 4 NANDs. The two additional pins supply power (+5 V) and connect the ground.

Connecting output of gates to the input of other gates allows to build complex circuits which can perform various computational tasks, including arithmetic in the binary system. Below is a 4-bit multiplexer which depending on the value of selectors (S0, S1), forwards one of the inputs (I0, I1, I2, I3) to the output:

The truth table for this device:

Below is the 74181, a 4-bit ALU (arithmetic logic unit):

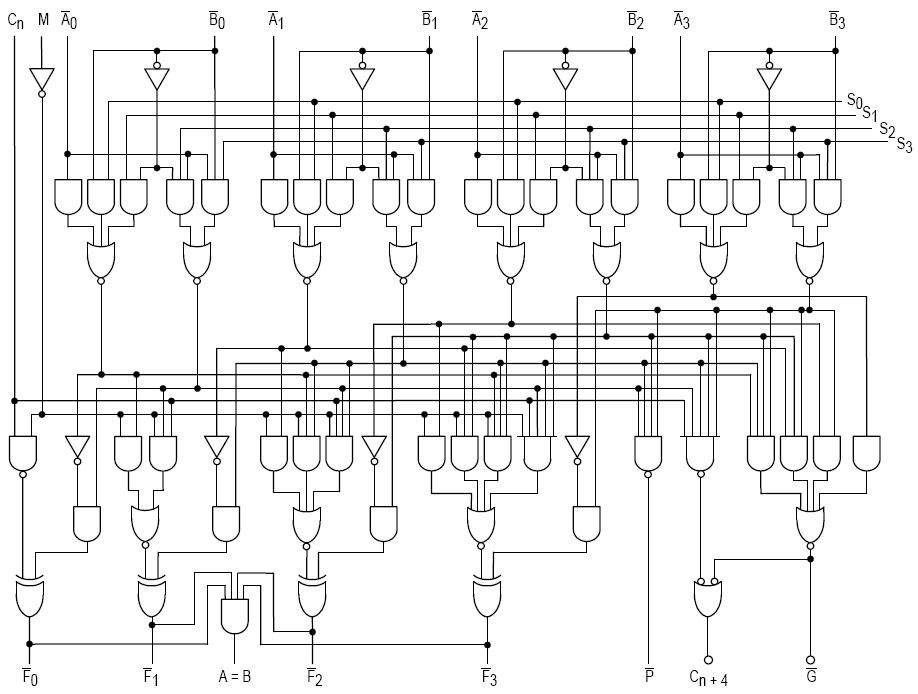
The device has many inputs:

• 4-bit data A (A0, A1, A2, A3)

• 4-bit data B (B0, B1, B2, B3)

• 4-bit function selector (S0, S1, S2, S3)

• Carry (Cn)

• Mode (M)

And many outputs:

• 4-bit function result (F0, F1, F2, F3)

• A = B bit

• Carry (C(n+4))

• propagate bit (P)

• generate bit (G)

Selectors decide what the ALU is doing. Since there are 4 selection bits, the device can perform 2^4 = 16 different functions (which means 16 truth tables for inputs A and B), each with specific Mode and Carry. Some of possible operations are:

• addition of 2 4-bit integers (first integer represented in binary system by A inputs, second by B) (if sum does not fit in 4 bits it's signaled through Carry output)

• subtraction of 2 4-bit integers (if result is negative it's signaled through Carry output)

• bitwise logical operations (e.g. F0 = A0 XOR B0, F1 = A1 XOR B1, ...)

• bit shift operations (e.g. F0 = 0, F1 = A0, F2 = A1, F3 = A2)

At this point you should understand how computers work. Modern hardware is made of highly-integrated circuits which can contain billions of transistors.